اختبارات الفروض الإحصائية في 8 خطوات مهمة

اختبارات الفروض الإحصائية

اختبارات الفروض الإحصائية (Statistical Hypothesis Testing) تُعد أحد الركائز الأساسية في التحليل الإحصائي. تهدف هذه الاختبارات إلى اتخاذ قرارات مبنية على البيانات المتاحة فيما يتعلق بصحة فرضية معينة. يتم استخدام هذه الأداة في مجموعة واسعة من المجالات، بما في ذلك العلوم الطبيعية، الطب، الاقتصاد، والهندسة. كما تُستخدم لتقييم فعالية السياسات أو التجارب أو حتى التغيرات البيئية، من خلال تحديد ما إذا كانت النتائج الملحوظة ناتجة عن الصدفة أم تعكس أثراً حقيقياً. وبذلك، توفر اختبارات الفروض إطاراً علمياً لاتخاذ قرارات موضوعية مدعومة بالأدلة الإحصائية. وفي هذا المقال، سنستعرض المفاهيم الرئيسية المرتبطة باختبارات الفروض الإحصائية، بما في ذلك أنواع الفرضيات، مستويات الدلالة، أنواع الأخطاء، وأشهر الاختبارات المستخدمة.

 

ما هي الفرضية الإحصائية؟

الفرضية الإحصائية هي افتراض أو فرض يتم وضعه حول خاصية إحصائية معينة (مثل المتوسط، النسبة، أو التباين) في مجتمع إحصائي. يتم اختبار هذا الافتراض باستخدام بيانات عينة مأخوذة من المجتمع، بهدف تحديد ما إذا كان الافتراض صحيحًا أم لا.

 

ما هو اختبار الفروض الإحصائية؟

اختبار الفروض الإحصائية (Statistical Hypothesis Testing) هو إجراء إحصائي يُستخدم لاتخاذ قرار حول صحة فرضية معينة بناءً على البيانات المتاحة. يتم استخدام هذا الاختبار لتحديد ما إذا كانت النتائج التي تم الحصول عليها من عينة بيانات تدعم الفرضية المطروحة أم لا.

 

أنواع الفرضيات الإحصائية

يمكن استخلاص أنواع اختبارات الفروض الإحصائية التي يتم استخدامها في اختبارات الفروض الإحصائية. تنقسم الفرضيات الإحصائية إلى عدة أنواع رئيسية، وهي كالتالي:

أولا: الفرضية الصفرية (Null Hypothesis – H₀)

هي الفرضية التي تنص على عدم وجود فرق أو تأثير معنوي بين المتغيرات المدروسة. يتم افتراض صحتها مبدئيًا إلى أن تُثبت البيانات خلاف ذلك عند اختبارات الفروض الإحصائية
مثال:
H₀: μ₁ = μ₂ (أي أن متوسط المجموعتين متساويان).

الغرض: تُستخدم كنقطة انطلاق لاختبار الفرضيات، حيث تُعتبر صحيحة ما لم تظهر أدلة إحصائية كافية لرفضها.

ثانيا: الفرضية البديلة (Alternative Hypothesis – H₁)

هي الفرضية التي تفترض وجود فرق أو تأثير معنوي بين المتغيرات، وتُعد نقيضًا للفرضية الصفرية.
مثال:
H₁: μ₁ ≠ μ₂ (أي أن متوسط المجموعتين مختلفان).
الغرض: تُستخدم لتحديد ما إذا كانت البيانات تشير إلى علاقة ذات دلالة إحصائية بين المتغيرات.

ثالثا: الفرضيات البارامترية (Parametric Hypotheses)

تعتمد هذه الفرضيات على افتراضات حول خصائص المجتمع الإحصائي، مثل التوزيع الطبيعي للبيانات وتساوي التباينات.
أمثلة:

1. اختبار t
2. تحليل التباين (ANOVA)
3. اختبار الانحدار الخطي
4. الافتراضات:
   • البيانات تتبع توزيعًا طبيعيًا.
   • تساوي التباينات عند المقارنة بين مجموعات.

رابعا: الفرضيات اللابارامترية (Nonparametric Hypotheses)

لا تعتمد على افتراضات محددة حول توزيع البيانات، وتُستخدم في حال كانت البيانات غير طبيعية أو رتبية
أمثلة:

1. اختبار Mann-Whitney
2. اختبار Kruskal-Wallis
3. اختبار Wilcoxon Signed-Rank

الغرض: تعد بديلًا مناسبًا عندما لا تُحقق البيانات شروط الفرضيات البارامترية.

خامسا: الفرضيات الأحادية الطرف (One-Tailed Hypotheses)

تُستخدم عندما يكون الهدف هو التحقق من وجود فرق في اتجاه محدد فقط، إما بالزيادة أو النقصان.
مثال:
H₁: μ₁ > μ₂ (أي أن متوسط المجموعة الأولى أكبر من الثانية).
الغرض: تُناسب الحالات التي يكون فيها التوقع موجّهًا نحو اتجاه واحد.

سادسا: الفرضيات ثنائية الطرف (Two-Tailed Hypotheses)

تُستخدم لاختبار الفرق في كلا الاتجاهين، سواء بالزيادة أو النقصان.
مثال:
H₁: μ₁ ≠ μ₂ (أي أن متوسط المجموعة الأولى يختلف عن الثانية دون تحديد الاتجاه).
الغرض: تُستخدم عندما لا يكون هناك افتراض مسبق حول اتجاه الفرق بين المجموعات.

سابعا: الفرضيات المتعلقة بالنسب (Proportion Hypotheses)

1. تُستخدم لاختبار الفروق بين نسب مئوية أو نسبتين ضمن بيانات فئوية.
   أمثلة:
   اختبار النسبة الواحدة
   اختبار الفرق بين نسبتين
   الغرض: مناسبة لتحليل البيانات الفئوية (Categorical Data)، مثل النسبة المئوية للمستجيبين.

ثامنا: الفرضيات المتعلقة بالتوزيعات (Distribution Hypotheses)

تُستخدم لتحديد ما إذا كانت البيانات تتبع توزيعًا معينًا مثل التوزيع الطبيعي.

أمثلة:

1. اختبار Kolmogorov-Smirnov
2. اختبار Shapiro-Wilk

الغرض: التحقق من مدى ملاءمة البيانات لتوزيع إحصائي محدد، وهو أمر مهم لاختيار نوع الاختبار الإحصائي المناسب.

تاسعا: الفرضيات المتعلقة بالارتباط (Correlation Hypotheses)

تُستخدم لقياس وجود علاقة بين متغيرين أو أكثر، من حيث القوة والاتجاه.
أمثلة:

1. اختبار الارتباط الخطي (Pearson)
2. اختبار الارتباط الرتبي (Spearman)

الغرض: تحديد مدى ترابط المتغيرات، وهو مفيد في الدراسات التفسيرية أو التنبؤية.

عاشرا: الفرضيات المتعلقة بالتنبؤ (Prediction Hypotheses)

تُستخدم لاختبار كفاءة نماذج التنبؤ الإحصائية في تفسير السلوك المستقبلي للمتغيرات.
أمثلة:

1. اختبار الانحدار الخطي
2. اختبار نماذج التنبؤ الزمني

الغرض: تقييم دقة النماذج في توقع نتائج مستقبلية، ويُعد ذلك محورًا أساسيًا في التحليلات التطبيقية.

 

أنواع اختبارات الفروض الإحصائية

تُعد اختبارات الفروض الإحصائية أدوات أساسية في التحليل الإحصائي لتحديد دلالة النتائج المستخلصة من البيانات. وتنقسم هذه الاختبارات إلى عدة أنواع رئيسية وفقًا لطبيعة البيانات والغرض من التحليل:

1-  الاختبارات البارامترية (Parametric Tests):

تُستخدم عندما تتبع البيانات توزيعًا طبيعيًا وتُحقق افتراضات محددة مثل تساوي التباين.
أمثلة:

1. اختبار t (لعينة واحدة، عينتين مستقلتين أو مرتبطتين)
2. تحليل التباين (ANOVA)
3. اختبار الانحدار الخطي

2-  الاختبارات اللابارامترية (Nonparametric Tests):

تُستخدم عند عدم تحقق الافتراضات البارامترية أو مع البيانات الرتبية والفئوية.
أمثلة:

1. اختبار Mann-Whitney
2. اختبار Kruskal-Wallis
3. اختبار Wilcoxon
4. اختبار Friedman
5. اختبار العشوائية (Runs Test)

3- اختبارات كاي-تربيع (Chi-Square Tests):

تُستخدم لتحليل العلاقات بين المتغيرات الفئوية أو اختبار مدى مطابقة التوزيع.
أنواع:

1. اختبار الاستقلالية
2. اختبار حسن المطابقة

4- اختبارات التوزيع

تُستخدم لاختبار مدى توافق البيانات مع توزيعات إحصائية محددة.

أمثلة:

1. اختبار Kolmogorov-Smirnov
2. اختبار Shapiro-Wilk

5- اختبارات الارتباط

لقياس قوة واتجاه العلاقة بين المتغيرات.

أمثلة:

Pearson Correlation

Spearman Rank Correlation

6- اختبارات النسب

تحلل الفروق بين النسب ضمن عينات.

أمثلة:

1. اختبار النسبة الواحدة
2. اختبار الفرق بين نسبتين

7- اختبارات التباين

تُستخدم لتقييم تساوي التباينات بين المجموعات.

أمثلة:

1. اختبار Levene
2. اختبار F

8-  اختبارات العينات الصغيرة

مناسبة للعينات المحدودة الحجم.

أمثلة:

1. t للعينة الواحدة
2. Wilcoxon Signed-Rank

9- اختبارات التصميم التجريبي

تحلل البيانات الناتجة عن تصميمات تجريبية محددة

أمثلة:

1. Fisher’s Exact Test
2. Cochran’s Q Test

10-  اختبارات التنبؤ

تُستخدم لتقييم دقة النماذج التنبؤية

أمثلة:

1. اختبار التنبؤ الخطي
2. اختبارات السلاسل الزمنية

 

خطوات إجراء اختبار الفرضية

تُعد اختبارات الفروض الإحصائية أداة منهجية تساعد الباحث في اتخاذ قرارات مبنية على البيانات المتاحة، من خلال تقييم صحة فرضية معينة حول المجتمع الإحصائي. وتعتمد هذه العملية على مجموعة خطوات منظمة تضمن الوصول إلى نتائج دقيقة وموضوعية. فيما يلي الخطوات الأساسية لإجراء اختبار الفرضية:

أولا: تحديد الفرضيات (Formulating the Hypotheses)

تُصاغ كل من الفرضية الصفرية والفرضية البديلة استنادًا إلى صيغة السؤال البحثي، حيث تُترجم المشكلة البحثية إلى فرضيات قابلة للاختبار الإحصائي، بما يسمح بتقييم العلاقة أو الفرق بين المتغيرات محل الدراسة.

ثانيا: اختيار مستوى الدلالة (Significance Level – α)

هو احتمال ارتكاب خطأ من النوع الأول، أي رفض الفرضية الصفرية وهي صحيحة. تُستخدم عادةً قيم مثل 0.05 أو 0.01. يُتخذ القرار بناءً على المقارنة بين القيمة الاحتمالية (P-Value) ومستوى الدلالة:

إذا كانت P-Value < α، تُرفض H₀.

إذا كانت P-Value ≥ α، لا تُرفض H₀.

ثالثا: جمع البيانات واختيار الاختبار المناسب

بعد تحديد الفرضيات أثناء اختبارات الفروض الإحصائية، يتم جمع البيانات وتحليلها باستخدام اختبار إحصائي ملائم، وذلك وفقًا لطبيعة المتغيرات، ونوع البيانات، وتصميم الدراسة. يُسهم اختيار الاختبار المناسب في ضمان دقة النتائج وقابليتها للتفسير الإحصائي الصحيح. من أبرز الاختبارات المستخدمة:

1. اختبار t (t-Test): يُستخدم لمقارنة متوسطَي مجموعتين مستقلتين أو مرتبطتين.
2. اختبار كاي تربيع (Chi-Square Test – χ²): يُستخدم لاختبار العلاقة بين متغيرين فئويين، وتحديد ما إذا كانا مستقلين إحصائيًا.
3. تحليل التباين (ANOVA): يُستخدم عند مقارنة متوسطات ثلاث مجموعات أو أكثر لتحديد ما إذا كانت هناك فروق ذات دلالة إحصائية بينها.

رابعا: حساب القيمة الإحصائية

يتم حساب القيمة الإحصائية عند اختبارات الفروض الإحصائية بناءً على البيانات المتاحة باستخدام الصيغ الرياضية الخاصة بكل اختبار إحصائي.

 اختبار t (t-Test):

تُحسب القيمة باستخدام الصيغة التالية:

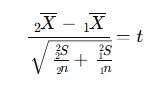
حيث:

 اختبار كاي تربيع (Chi-Square Test – χ²)

تُحسب القيمة باستخدام الصيغة التالية:

 

خامسا: تحديد القيمة الحرجة (Critical Value)

تُحدد القيمة الحرجة باستخدام الجداول الإحصائية المناسبة أو من خلال برامج تحليل إحصائي مثل Minitab، وذلك بناءً على مستوى الدلالة α ودرجات الحرية (Degrees of Freedom – DF).

1. إذا كانت القيمة المحسوبة (Test Statistic) أكبر من القيمة الحرجة، يتم رفض الفرضية الصفرية H₀.
2. إذا كانت القيمة المحسوبة أصغر من أو تساوي القيمة الحرجة، يتم قبول الفرضية الصفرية H₀

سادسا: اتخاذ القرار (Decision Making)

بناءً على مقارنة القيمة المحسوبة مع القيمة الحرجة أو مقارنة P-Value مع α، يتم اتخاذ القرار الآتي عند اختبارات الفروض الإحصائية:

1. رفض الفرضية الصفرية H₀: إذا كانت النتائج دالة إحصائيًا (Statistically Significant)، أي أن القيمة المحسوبة تتجاوز القيمة الحرجة أو أن P-Value أقل من α.
2. قبول الفرضية الصفرية H₀: إذا كانت النتائج غير دالة إحصائيًا، أي أن القيمة المحسوبة أقل من أو تساوي القيمة الحرجة أو أن P-Value أكبر من أو يساوي α.

سابعا: تفسير النتائج (Interpretation)

يتم تقديم تفسير واضح وبسيط للنتائج عند اختبارات الفروض الإحصائية بما يتماشى مع السياق البحثي

مثال:

1. لا يوجد دليل كافٍ لرفض الفرضية الصفرية، مما يعني أن المتوسطات متساوية.”
2. “هناك دليل كافٍ لرفض الفرضية الصفرية، مما يعني وجود فرق معنوي بين المتوسطات.”

ثامنا: استخدام البرامج الإحصائية

يمكن استخدام برامج مثل Minitab في اختبارات الفروض الإحصائية لإجراء الحسابات بسهولة
مثال:

 

الخاتمة

ختامًا، تُعد اختبارات الفروض الإحصائية عنصرًا أساسيًا لا غنى عنه في البحث العلمي والإحصائي، إذ تسهم في تقديم أدلة كمية موضوعية تدعم اتخاذ القرارات وتفسير الظواهر المدروسة. ويُعد الإلمام بمبادئ هذه الاختبارات، من حيث صياغة الفرضيات واختيار الاختبار المناسب وتحليل النتائج، أمرًا بالغ الأهمية لضمان دقة التفسير وموثوقية النتائج. كما أن الاستخدام الصحيح لهذه الأدوات يعزز من قوة الاستنتاجات البحثية ويُسهم في بناء معرفة علمية رصينة يمكن الاعتماد عليها في مجالات متعددة، سواء في العلوم الطبيعية أو الاجتماعية أو التطبيقية